The summer of 2016 overflowed with extreme rain events. Here at Climate.gov, we’ve written about two of them: the June floods in southern West Virginia and the mid-August floods in Louisiana.
After the historic flooding in West Virginia in June, the National Weather Service said that in parts of West Virginia, 24-hour rainfall amounts—more than 10 inches in some places—were a thousand-year event. We often do not have observations that go back 100 years, let alone 1,000. So how do scientists figure that out? The answer lies in statistics.
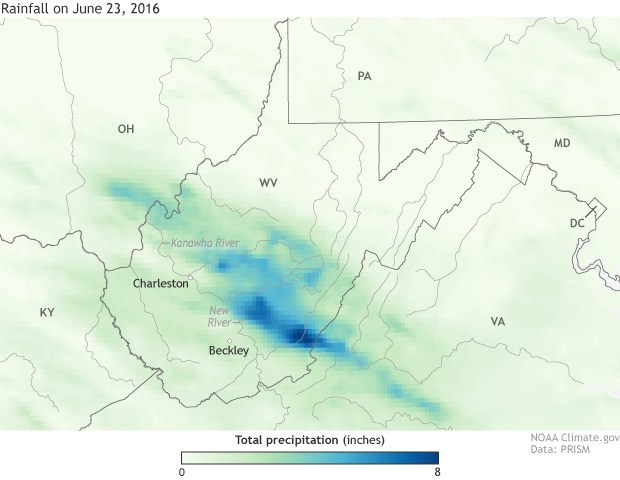
An "early glimpse" of 24-hour rainfall totals from storms over West Virginia on June 23, 2016, based on PRISM data from Oregon State University. "Early glimpse" data may not include data from all stations in the reporting network, and totals should be considered preliminary. Even the preliminary totals are enormous, however, with up to 8 inches of rain in many areas of southeastern West Virginia. Map by NOAA Climate.gov.
Dinosaurs and data
Estimating the size of a thousand-year event using a much shorter history of observations is like how paleontologists can take an incomplete collection of fossilized Tyrannosaurus Rex bones and turn them into a picture of what T-rex probably looked like when alive. The climate “bones” are all the observations we have. Since we have an admittedly incomplete set of weather observations, we have to use what we’ve got to create an image of the actual climate “dinosaur.”
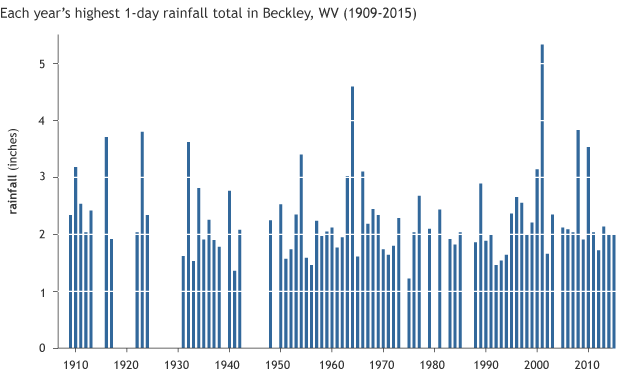
Let’s work through it with a real-life example. I have compiled over 80 years’ worth of daily rainfall observations from the Beckley VA Hospital in West Virginia, near where June rains were so extraordinary. First, I eliminated any year with more than 10 days of missing data. Next, I pulled the highest daily rainfall amount that occurred in each year (1). Some years clearly have larger daily rainfall maximums than others.
Annual maximum daily precipitation totals from 1909 to 2015 at a weather station located at Beckley VA Hospital in West Virginia. Years where more than 10 days of precipitation data were missing are excluded. NOAA Climate.gov based on data from the National Centers for Environmental Information.
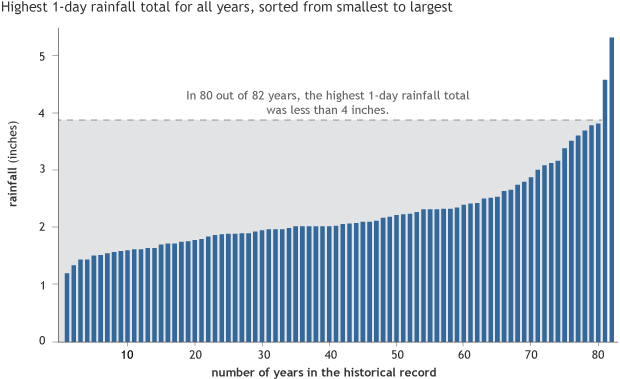
To figure out how rare a particular rainfall event was, we need to understand the range of the data. We’ll start by putting the values in order from smallest to largest.
Annual maximum precipitation totals (inches) sorted from smallest to largest for 82 years at Beckley VA hospital in Beckley, West Virginia. The annual maximum precipitation total exceeded 4 inches in only two of the 82 years. NOAA Climate.gov map based on station data from the National Centers for Environmental Information.
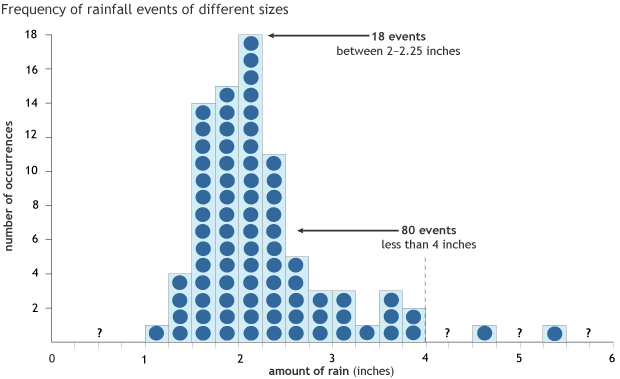
Ordering the data from lowest to highest allows us to see the spread in totals but doesn’t help us figure out what is the most common daily rainfall maximum. For that, we need to sort the values into bins defined by rainfall amount (a bin for 0 inches, 0-0.25, 0.25-0.5 inches etc), like sorting clothes into piles based on size. It is at this step, that we can begin to see if there is a pattern.
A histogram of annual daily maximum precipitation totals for Beckley, West Virginia. There are 82 years in total. Precipitation totals are sorted into 0.25-inch bins. The most common bin, with 18 events, represented daily precipitation totals between 2 and 2.25 inches. 80 of the 82 years had precipitation amounts less than 4 inches. NOAA Climate.gov figure based on data from the National Centers for Environmental Information.
Certain piles have more items of clothing in them than others: we have more mediums than extra-larges so to speak. It is clear that some yearly 24-hour rainfall maximums occur more often than others. In 18 of 80 years, the highest 24-hour rainfall was between 2 and 2.25 inches. In 15 years, the highest daily rainfall total was between 1.75 and 2.0 inches. Only one time in 80 years was there a daily record above 5 inches.
However, the other thing that is clear is that the spread is incomplete. In this example, there are no years in which the highest daily rainfall total was between 4 and 4.5 inches, but there are some cases between 4.5-4.75 inches and 5.25-5.5 inches. It’s not physically plausible that the atmosphere would just never produce those rain amounts. It’s more logical to assume that if we had enough data going far enough back or forward in time, that there would eventually be a daily event filling in the gaps.
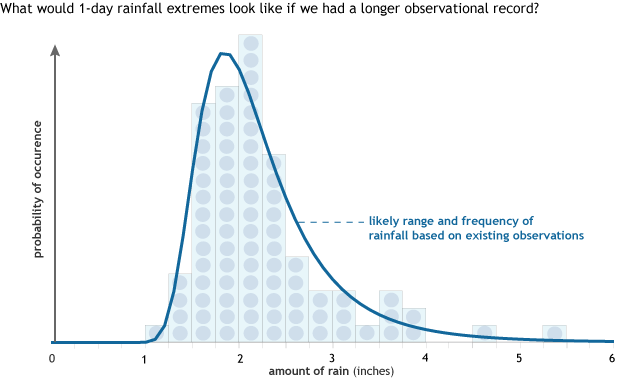
This is where statistics come in. Scientists apply what they call a “distribution” (the dark line in the figure below), a relationship of the magnitude of the rainfall to how often that rainfall amounts occurs (2). The distribution line is like the final picture of the dinosaur. It uses the observations (bones) as the input for a reconstruction of the whole climate picture.
The observations from Beckley, WV, of the frequency of rain events of different sizes (dots inside bars) can be used to estimate the full range of likely events and their frequency (dark line). This statistical estimate is called the probability density function, and it's like the process of using the bones from an incomplete dinosaur skeleton to describe what the complete creature probably looked like. Graph by NOAA Climate.gov, based on data from NCEI.
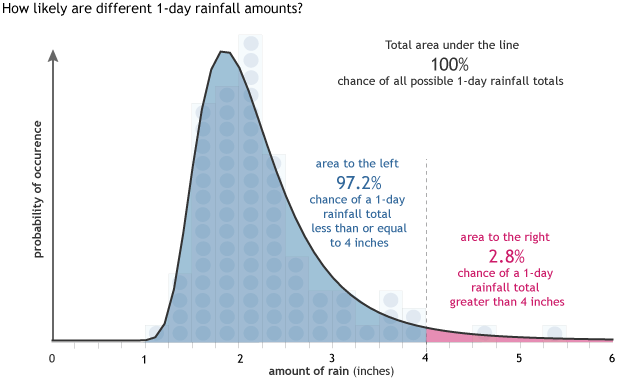
And now, researchers can see how often an event of any rainfall amount is likely to occur. In fact, if we consider the total area under the curve (dark line) and recognize that it must equal 1.0 (100%), then the probability of a single event of a given size occurring at some point is simply the area under that portion of the curve. The probability of a yearly daily maximum rainfall event greater than 4 inches, for example, is just the area from 4 on the x-axis to the right, bounded by the distribution line.
In this type of graph, the curved line marks a hypothetical list of all possible extreme rainfall events, with the caveat that the total area under the curved line must equal 1.0 or 100%. The percent chance of any single rain event being more than a specific amount is the percent of the total area to the right of that rainfall amount. The percent chance of a rain event less than or equal to that threshold can be found by subtracting the area to the right of the threshold from 100. Graph by NOAA Climate.gov.
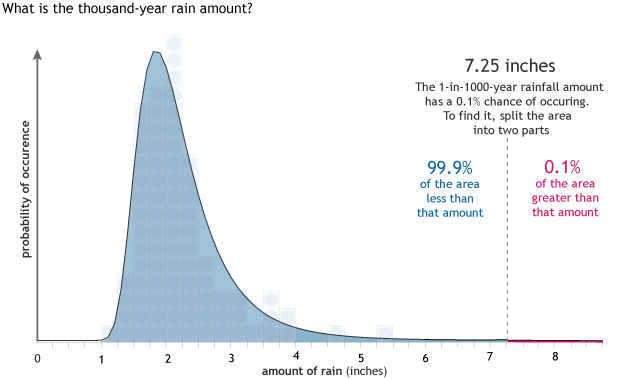
Since we can figure out the probability for a given rainfall amount, we can also figure out what rainfall amounts correspond to specific probabilities like 0.1%, or said another way, a 1-in-1,000 year event (1/1000).
Using the area under the line, we can also flip the calcuation. Instead of finding the percent chance of an event of a certain size, we can find the amount of rain associated with an event of a certain probability. In Beckley, WV, the amount of rain associated with an event that has 0.1% chance of ocurring is 7.25 inches. Because a 0.1% chance is the same as 0.001, or 1 in 1,000, such events have been nicknamed "thousand-year" events." Graph by NOAA Climate.gov.
Is the statistical estimate perfect? Of course not. There are many different types of distributions used for different variables, depending on what assumptions you make about the phenomenon you’re talking about. You can even use different distributions for the same variable like precipitation! The distribution is an assumption, after all. And for events which are very rare, there is a great deal of uncertainty. Small differences in what a distribution line looks like at the extremes can have large impacts on the probabilities of uncommon events.
Therefore, scientists can be more confident in the rainfall amounts needed for a 1-in-100-year storm than a 1-in-1,000-year event, and they often don’t even bother to estimate out beyond that. This story's example, in particular, is a much simpler version of the more complex work already done by NOAA scientists.
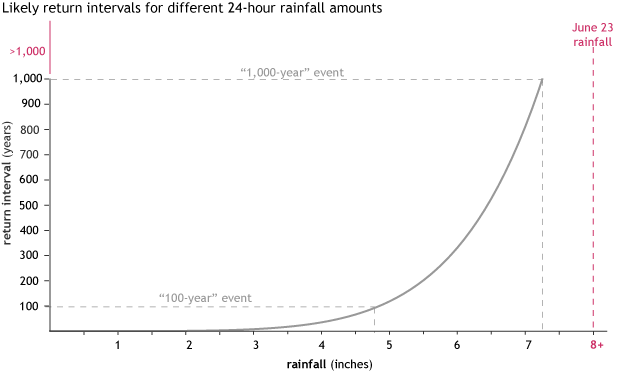
The return periods (0 to 1000 years) for rainfall amounts from 0 to over 7 inches based on 82 years of annual daily maximum precipitation data from Beckley, West Virginia. A 1 in 1000 year event, as calculated using the basic statistical technique of applying a distribution, would mean daily rainfall amounts of over 7 inches. During the event just north of this location on June 23, 2016, over 8 inches of rain fell in some locations in just 24 hours. NOAA Climate.gov figure based on data from the National Centers for Environmental Information.
To bring it back to the dinosaur picture, when I was growing up, dinosaurs had no feathers. Nowadays, feathered dinosaurs are much more widely accepted. What happened? More data and a better understanding led to a change in the picture (or the distribution, if we are talking rain). The same can happen here. More observations and research can help fine tune the climate picture.
Wait I’m still not sure I understand what a 1-in-1,000-year event means
At the start of every school year, I used to guess what the chances of extreme weather events that year would be. As a typical kid, I remember always guessing (or hoping) that there was a 50% chance we would get a foot of snow at some point that winter that would cancel school. But I have no control over the likelihood of extreme events; only Mother Nature does (disregarding for a second how human-caused climate change can affect things).
There are different chances for all possible weather events. What the distribution shows us is that some events are more likely than others. There is a high chance, for instance, that at some point in the next year it rains more than 0.25 inches in West Virginia. There are also events that are so extreme that their chance of occurring in any given year is pretty small. If an event has only a 1% chance of happening in a year, that is equivalent to 1 divided by 100, or said another way a 1-in-100-year storm. A one-in-a-thousand year event would have a 0.1% chance (1 divided by 1,000) of occurring in any given year.
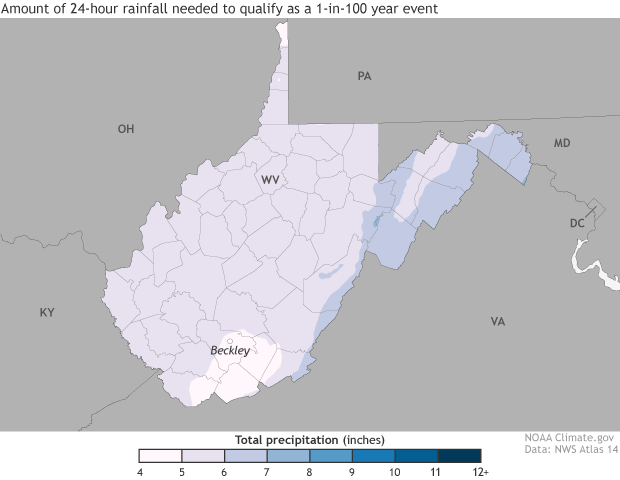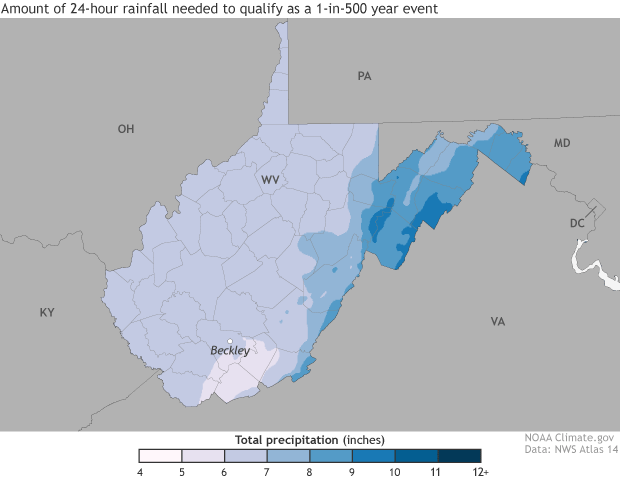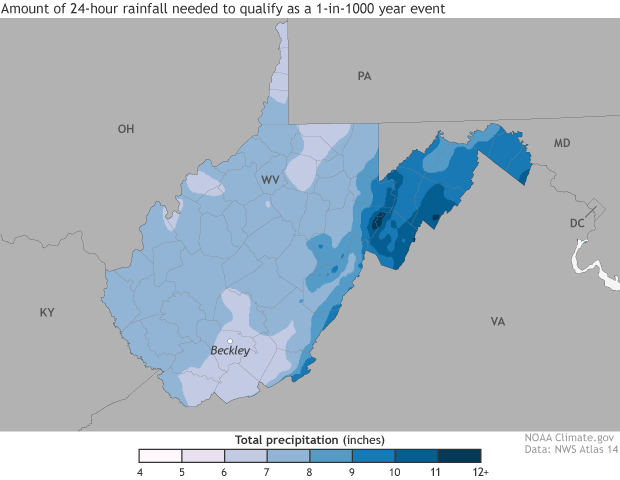
The 1-day rainfall amounts that have have a 1%, 0.5%, or 0.1% chance of occuring each year. Over very long periods of time, such events are likely to occur with an average frequency of 1-in-100, 1-in-500, or 1-in-1,000 years. Maps and animation by NOAA Climate.gov, based on NOAA Atlas 14 data.
Importantly, this is not saying that if a thousand-year event occurs that you have to wait another 1,000 years for the next one. There can be multiple events of that magnitude within 1,000 years or none. All that is being said is that there is a 0.1% chance of that event occurring in any given year. We can even calculate the probability that a thousand-year event will occur during an arbitrary millennium. If there is a 0.1% chance the event occurs in any year, it also means there is a 99.9% chance it won’t. The probability of not seeing the event 1,000 years in a row would be equal to 0.999 (99.9%) raised to the 1000th power (# of years), which equals a 36.8% chance that the 1-in-1000-year event will not occur during any single randomly chosen 1,000-year time period, and a 63.2% chance that it will.
Climate change probably messes with this, right?
Yup. When scientists are attempting to paint a picture of the climate using past observations, it is best if the climate is not changing that much. A changing climate means relying on a past that may not be as helpful. In fact, global warming can shift the natural distribution of a climate variable entirely.
For instance, according to the special report on extreme weather issued in 2012 by the Intergovernmental Panel on Climate Change, it is likely that a 1 in 20 year extreme 24-hour precipitation events will become a 1 in 5 to 15 year event by the end of the century in many regions. The picture could change, which leaves scientists in a tough position of figuring out the rarity of extreme events on one hand, while recognizing that the chances of these events may already be changing due to climate change on the other.
Footnote
(1) Another approach is to gather all of the largest events without the limitation of one per year. For example, if we were looking at 80 years’ worth of data, we would select the 80 largest events regardless of whether they occurred in the same year or not. This will lead to a slightly different dataset of extreme rainfall events but for this exercise, the conclusion would not be changed.
(2) The y-axis here is showing values of the probability density function, which you can think of as frequency. Higher values mean more occurrences. The numbers themselves don’t matter as much as the line seen on the plot. The key feature of this plot is that the area underneath the dark black line equals 1.0 (1.0 in this case can be thought of as 100%). To determine the probability of an event occurring, the area under that portion of the curve equals the probability.